| 英文 | 和訳 |
|---|---|
 |
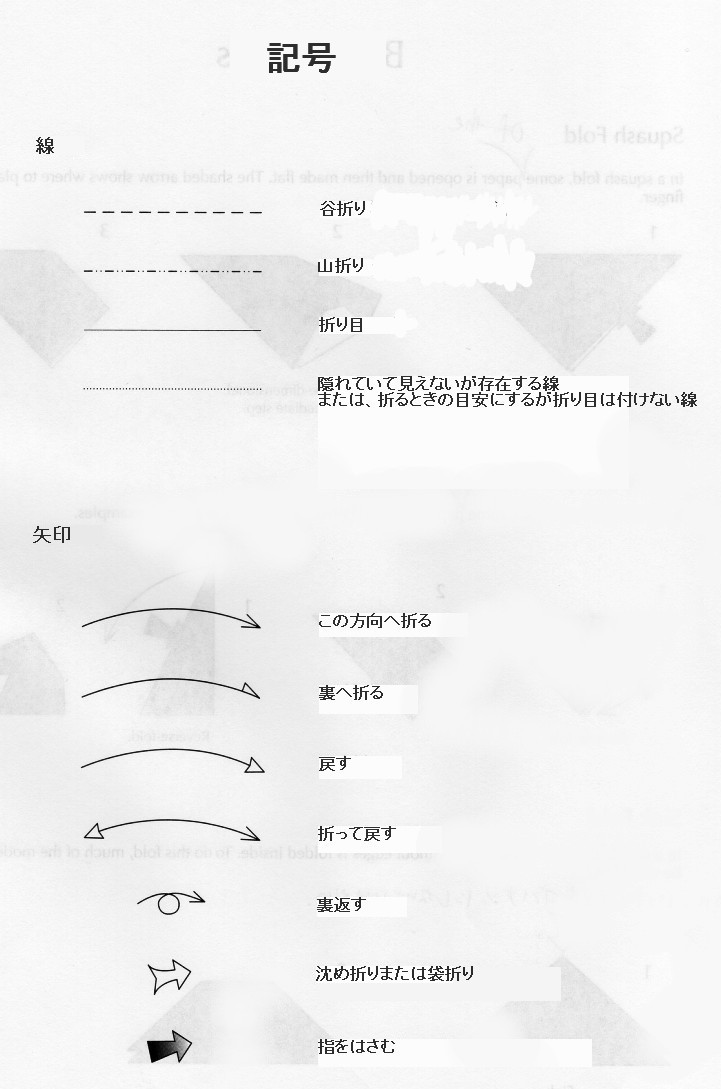 |
| Symbols | 記号 |
| Lines | 線 |
| Valley fold, fold in front. | 谷折り |
| Mountain fold, fold behind. | 山折り |
| Crease line. | 折り目 |
| X-ray or guide line. | 隠れていて見えないが存在する線 または、折るときの目安にするが折り目は付けない線 |
| Arrows | 矢印 |
| Fold in this direction. | この方向へ折る |
| Fold behind. | 裏へ折る |
| Unfold. | 戻す |
| Fold and unfold. | 折って戻す |
| Turn over. | 裏返す |
| Sink or three-dimensional folding. | 沈め折りまたは袋折り |
| Place your finger between these layers. | 指をはさむ |
 | 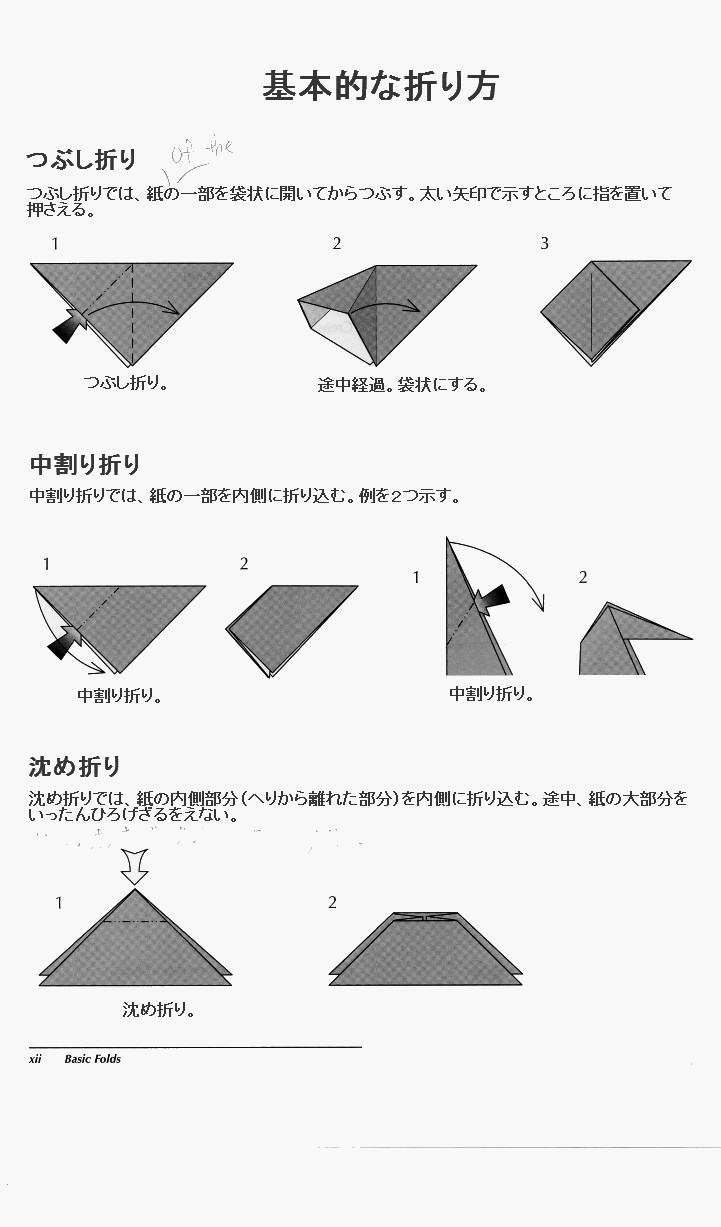 |
| Basic Folds | 基本的な折り方 |
| Squash Fold | つぶし折り |
| In a squash fold, some of the paper is opened and then made flat. The shaded arrow shows where to place your finger. | つぶし折りでは、紙の一部を袋状に開いてからつぶす。太い矢印で示すところに指を置いて押さえる。 |
| Squash-fold. | つぶし折り。 |
| A three-dimensional intermediate step. | 途中経過。袋状にする。 |
| Inside Reverse Fold | 中割り折り |
| In an inside reverse fold, some of the paper is folded between layers. Here are two examples. | 中割り折りでは、紙の一部を内側に折り込む。例を2つ示す。 |
| Reverse-fold. | 中割り折り。 |
| Reverse-fold. | 中割り折り。 |
| Sink Fold | 沈め折り |
| In a sink fold, some of the paper without edges is folded inside. To do this fold, much of the model must be unfolded. | 沈め折りでは、紙の内側部分(へりから離れた部分)を内側に折り込む。途中、紙の大部分をいったんひろげざるをえない。 |
| Sink. | 沈め折り。 |
| Polyhedra Overview | 多面体について |
| Polyhedra are three-dimensional shapes composed of polygons, two-dimensional shapes composed of straight lines. | 多面体は、いくつかの多角形が集まって構成される立体形状である。 |
| Convex Polyhedra | 凸多面体 |
| Take any two points on the surface of a polyhedron and picuture a line connecting them. A polyhedron is convex if all such lines are either on the surface of the polyhedron or are completely inside the polyhedron. | ここにひとつの多面体があるとする。その多面体の表面で、適当に2つの点をとってみる。その2点を直線で結んでみる。そのようにしてできるすべての直線が、その多面体の表面にへばりついているかまたは内部にめり込むかのどちらかであれば、その多面体は「凸多面体」である。 |
| Concave Polyhedra | 凹多面体 |
| If there are any lines connecting two points on the surface that are outside the polyhedron, even partially, then the polyhedron is concave, or nonconvex. | 上記のようにしてできる直線の中に、多面体の外にはみ出すようなものが存在すれば、その多面体は「凹多面体」である。 |
| Platonic Solids | 正多面体 |
| A Platonic solid is a convex polyhedron composed of identical regular polygons with identical vertices. | 互いに合同ないくつかの正多角形が集まって構成され、なおかつその頂点がすべて互いに合同である凸多面体を、正多面体という。 |
| Thus, all of the edges are the same length, the same number of edges meet at each vertex, and all the faces are the same shape. | だから正多面体では、どの辺も同じ長さであり、どの頂点にも同じ数の辺が集まり、どの面も同じ形をしている。 |
| There are five Platonic solids: the tetrahedron, cube, octahedron, icosahedron, and dodecahedron. | 正多面体は、正四面体、正六面体、正八面体、正二十面体、および正十二面体の5つがある。 |
(English Source: ORIGAMI POLYHEDRA DESIGN by John Montroll)